Convolutional Neural Networks

F. Reverter, A. Sanchez, and E. Vegas

Introduction

Session Outline

1.What is computer vision?

2.Learning visual features

<!-- Convolution and Padding -->
<!-- Filters, Strides, and Channels -->

3. Convolutional Neural Networks

4. Building and Training CNNs

5. Applications of CNNs

What do we mean by computers vision?

We want computers that can see

We want to build computer systems able to see what is present in the world, but also to predict and anticipate events.

source: MIT Course, http://introtodeeplearning.com/, L3

DNN useful in computer vision systems

• Deep learning is enabling many systems to undertake a variety of computer vision related tasks.

source: MIT Course, http://introtodeeplearning.com/, L3

Facial detection and recognition

In particular it enables automatic feature extraction, something that before DNN used to require relevant human participation.

source: MIT Course, http://introtodeeplearning.com/, L3

Autonomous driving

source: MIT Course, http://introtodeeplearning.com/, L3

Medicine, biology. self care

source: MIT Course, http://introtodeeplearning.com/, L3

What computers see?

Images are numbers

• To a computer images, of course, are numbers.

• An (RGB) image is just a NxNx3 matrix of numbers [0,255]

source: MIT Course, http://introtodeeplearning.com/, L3

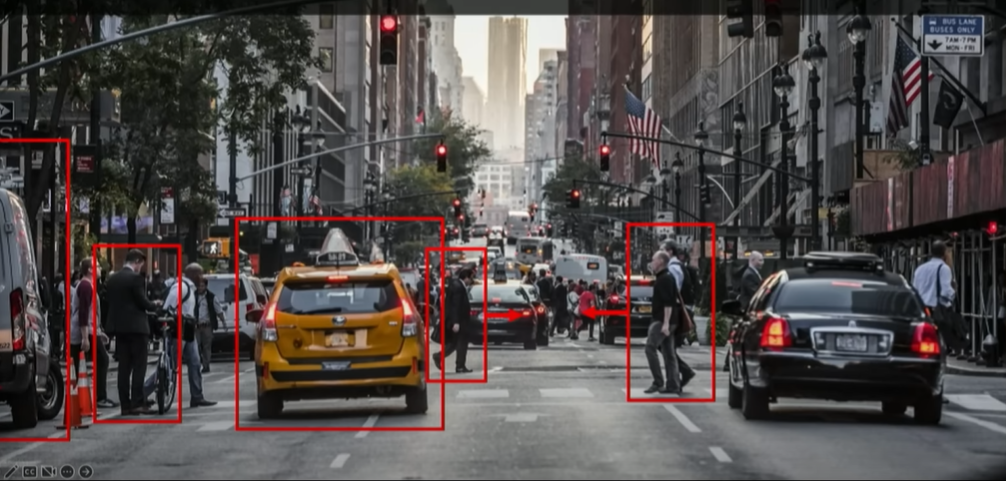
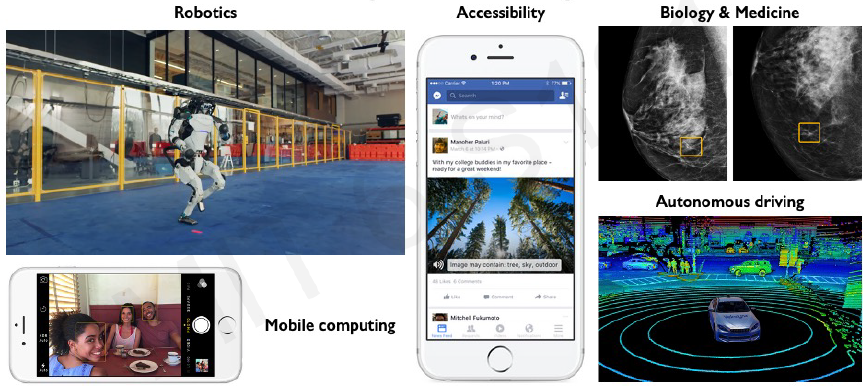
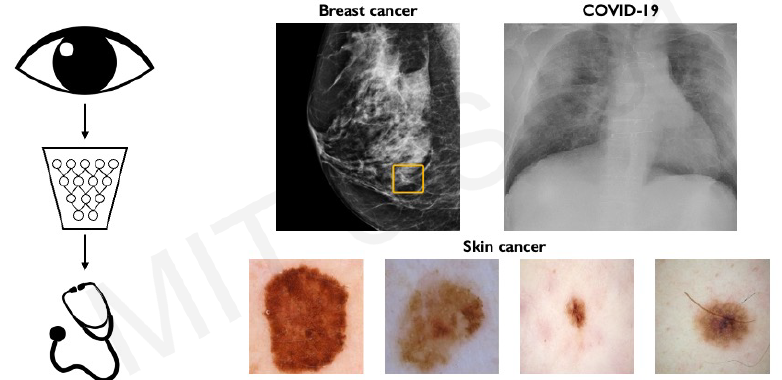
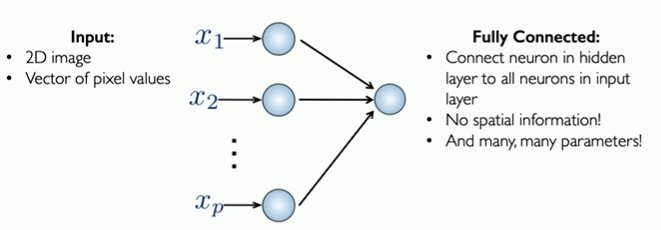
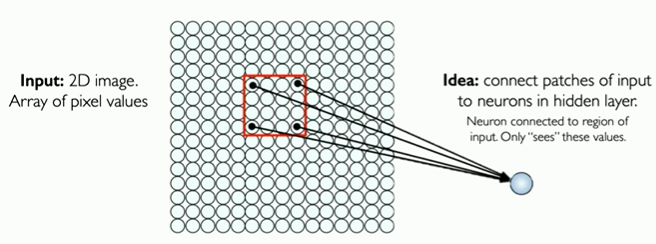
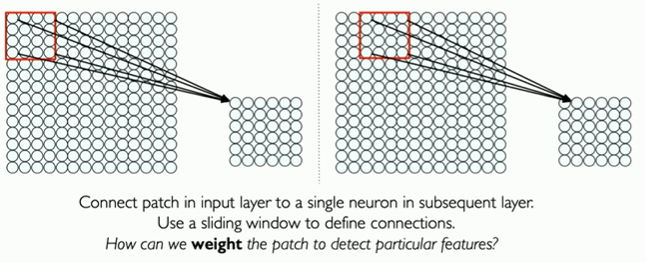
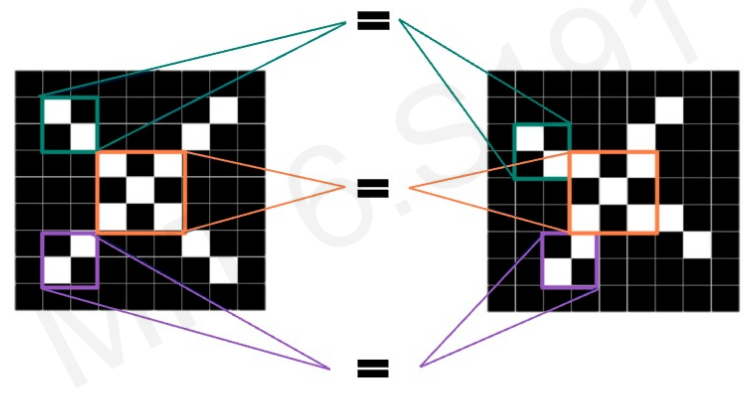
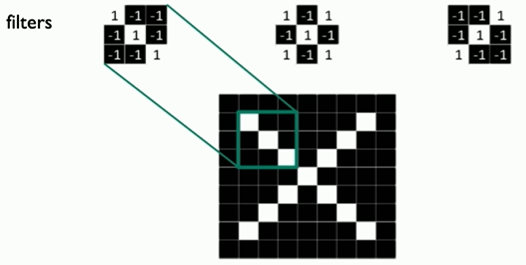
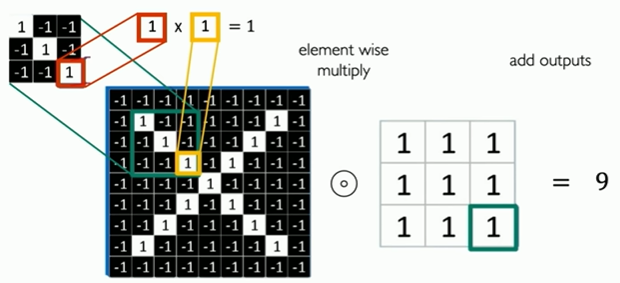
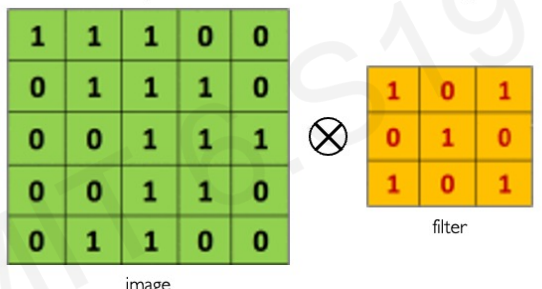
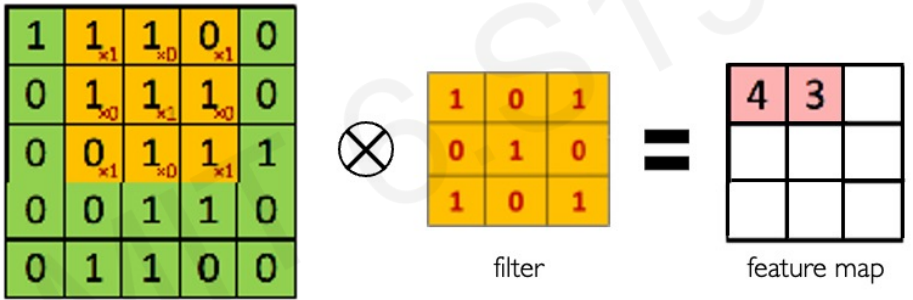
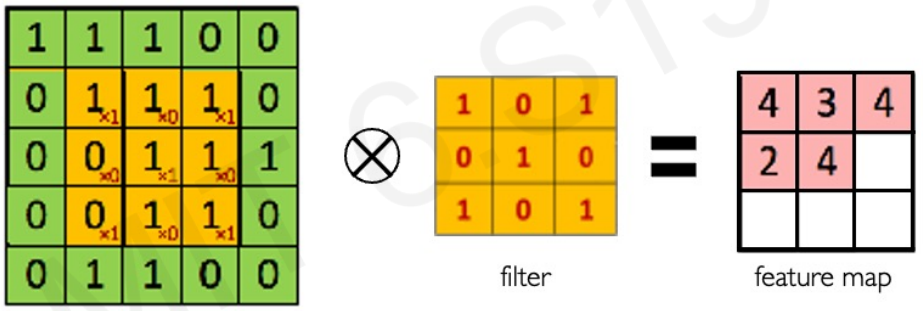
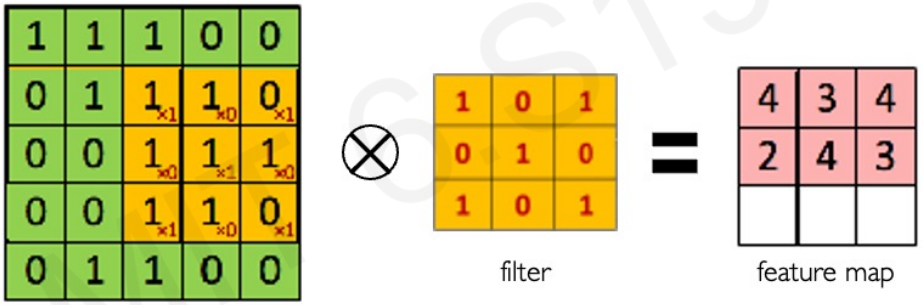
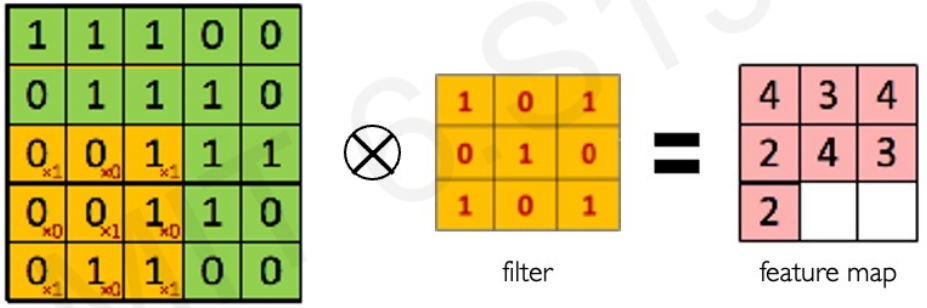
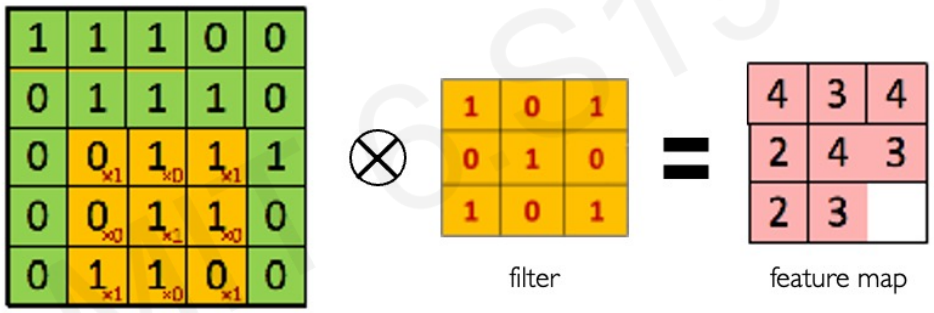
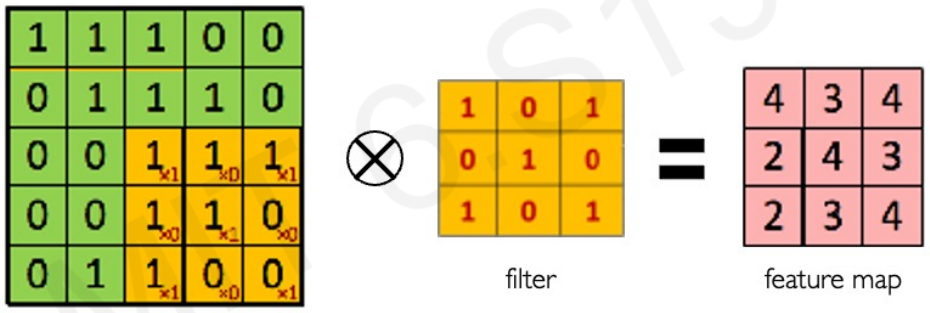
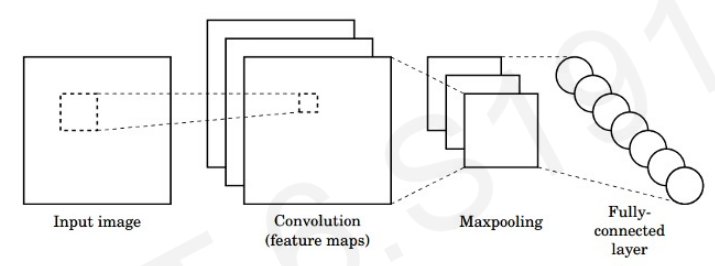
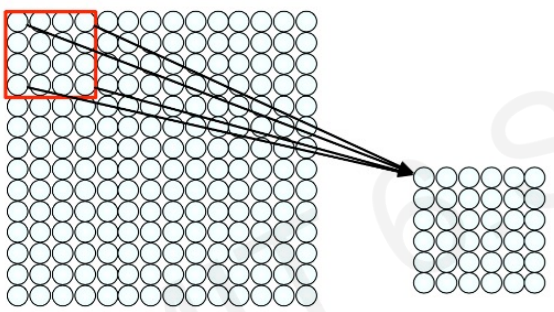
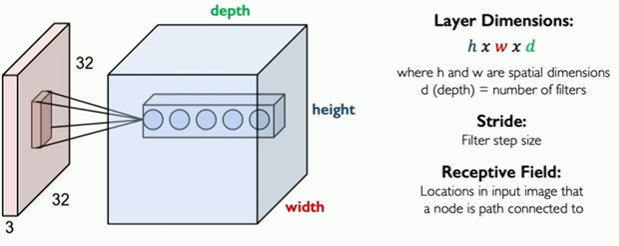
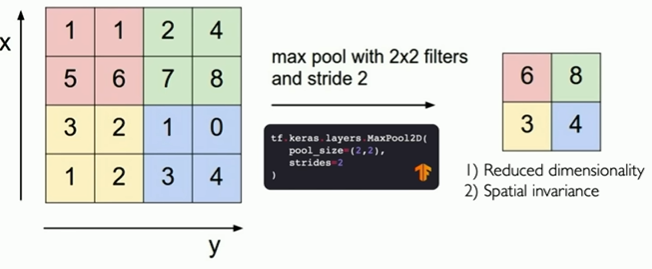
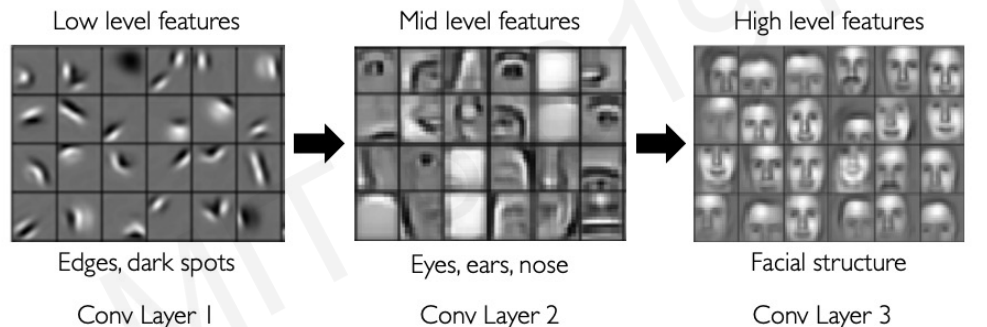
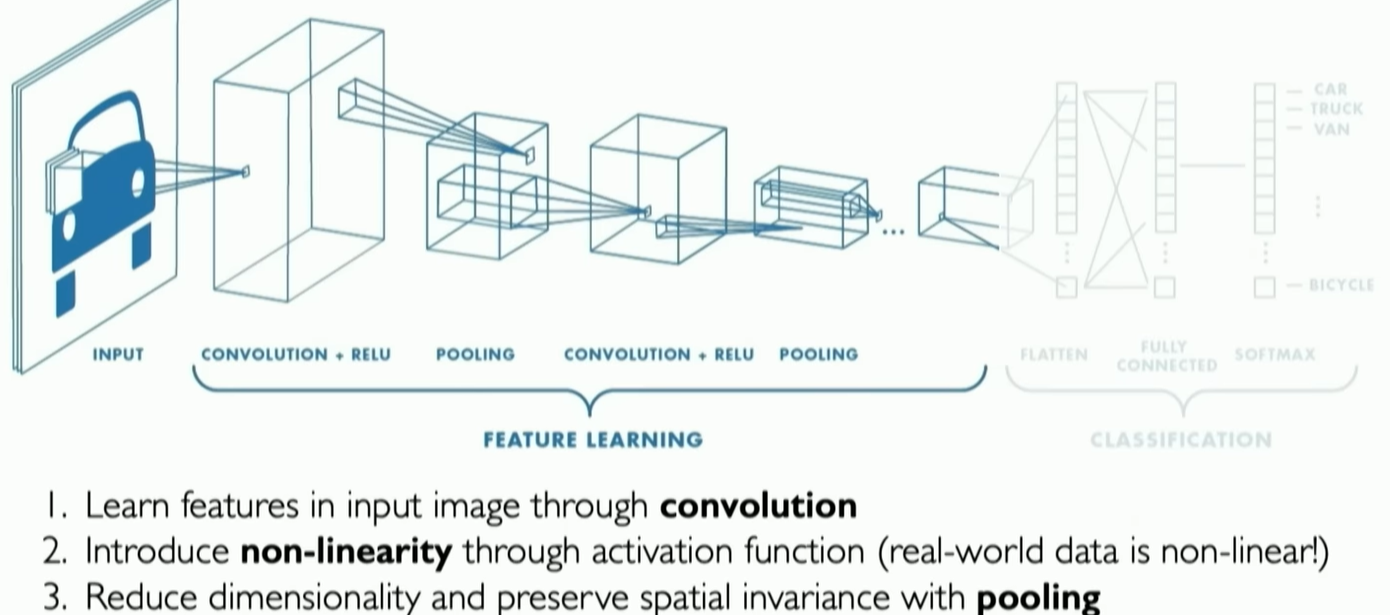
Main tasks in Computer Vision:

• Regression: Output variable takes continuous value. E.g. Distance to target
• Classification: Output variable takes class labels. E.g. Probability of belonging to a class

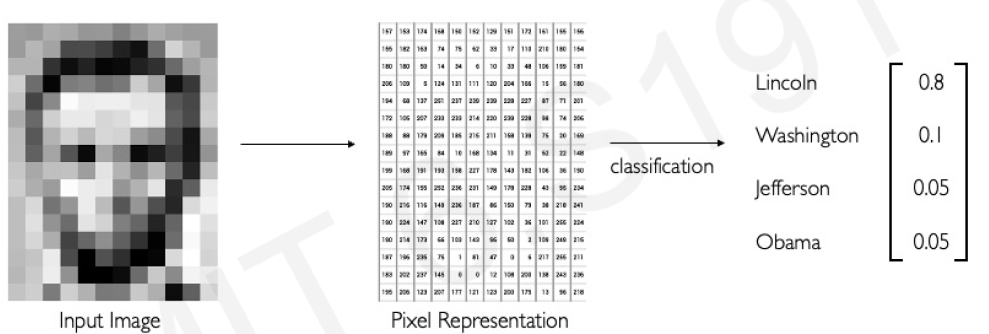
source: MIT Course, http://introtodeeplearning.com/, L3

High level feature detection

• Each image is characterized by a different set of features.

• Before attempting to build a computer vision system

• we need to be aware of what feature keys are in our data that need to be identified and detected.

source: MIT Course, http://introtodeeplearning.com/, L3

Manual feature extraction

• Manual feature extraction is hard! Especially if it has to be done “by hand”

source: MIT Course, http://introtodeeplearning.com/, L3

• Notice also that feature characterization needs to define a hierarchy of features that allowas an increasing level of detail

  HEAD -> Eyes/Mouth/Nose/… ->

Manual feature extraction

source: MIT Course, http://introtodeeplearning.com/, L3

Automatic feature extraction

• Can we learn a hierarchy of features directly from the data instead of hand engineering?

source: MIT Course, http://introtodeeplearning.com/, L3

• NN automatically learn features from the data
• They do it in a hierarchical fashion

Learning visual features

Feature extraction with dense NN

• Fully connected NN could, in principle, be used to learn visual features

source: MIT Course, http://introtodeeplearning.com/, L3

Accounting for spatial structure

• Images hav a spatial structure.
  • How could this be used to inform the architecture of the Network?

source: MIT Course, http://introtodeeplearning.com/, L3

Extending the idea with patches

source: MIT Course, http://introtodeeplearning.com/, L3

Use filters to extract features

• Filters can be used to extract local features

  • A filter is a set of weights

• Different features can be extracted with different filters.

• Filters that matter in one part of the input should matter elsewhere so:

  • Parameters of each filter are spatially shared.

Feature Extraction with Convolutions

source: MIT Course, http://introtodeeplearning.com/, L3

• A 4x4: 16 distinct weights filter is applied to define the state of the neuron in the next layer.
• Same filter applied to 4x4 patches in input
• Shift by 2 pixels for next patch.

Example: “X or X”?

source: MIT Course, http://introtodeeplearning.com/, L3

• Images are represented by matrices of pixels, so
• Literally speaking these images are different.

What are tye features of X

• Look for a set of features that:
  • characterize the images, and
  • and are the same in both cases.

source: MIT Course, http://introtodeeplearning.com/, L3

Filters can detect X features

source: MIT Course, http://introtodeeplearning.com/, L3

Is a given patch in the image?

• The key question is how to pick-up the operation that can take

  • a patch and
  • an image and

• An decide if the patch is in the image.

• This operation is the convolution.

The Convolution Operation

source: MIT Course, http://introtodeeplearning.com/, L3

• Convolution matches the patch and the image by elementwise multiplication, followed by a sum.
• Given the filters used (+1/-1) if there is absolute coincidence, as in the example, all multiplications will yield 1, and the sum will be 9.
• Two completely different patches would add -9.

The Convolution Operation

• Suppose we want to compute the convolution of a 5x5 image and a 3x3 filter.

source: MIT Course, http://introtodeeplearning.com/, L3

• We will slide the 3x3 filter over the input image, elementwise multiply and add the outputs

The Convolution Operation

1. slide the 3x3 filter over the input image,
2. elementwise multiply and (iii) add the outputs

source: MIT Course, http://introtodeeplearning.com/, L3

The Convolution Operation

1. slide the 3x3 filter over the input image,
2. elementwise multiply and (iii) add the outputs

Different filters for different patterns

• By applying differnt filters, i.e. changing the weights,
• We can achieve completely different results

Can filters be learned?

• Different filters can be used to extract different characteristics from the image.
  • Building filters by trial-and-error can be slow.
• If a NN can learn these filters from the data, then
  • They can be used to classify new images.
• This is what Convolutional Neural Networks is about.

Convolutional Neural Networks

CNNs: Overview

source: MIT Course, http://introtodeeplearning.com/, L3

1. Convolution: Apply filters to generate feature maps.

2. Non linearity: E.g. (ReLU) to deal with non linear data.

3. Pooling: Downsampling operations on feature maps.

Convolutional Layers

source: MIT Course, http://introtodeeplearning.com/, L3

Each neuron in the hidden layer:

• Takes inputs from the patch
• Computes weighted sum of elementwise products (“convolution”)
  • not dot operation
• Applies a bias.

• The single convolution operation can be extended from one neuron to one or more entire (hidden) layers of convolutions
• Remember: convolution does not interconnect all the neurons but only those in a patch.

• Local connectivity: Every single neuron only sees its patch

Convolutional Layers

For each neuron (\(p\), \(q\)) in the hidden layer:

• Take a 4x4 filter, a matrix of weights: \(w_{ij}\).
• Compute linear combinations; \[ \sum_{i=1}^4\sum_{j=1}^4 w_{ij} x_{i+p,j+q}+b \]
• Activate with non-linear function.

CNNs output volume

• Multiple filters can be applied on the same image.
  • Think of the output as a volume.

source: MIT Course, http://introtodeeplearning.com/, L3

Non linear activation

source: MIT Course, http://introtodeeplearning.com/, L3

Pooling

source: MIT Course, http://introtodeeplearning.com/, L3

Pooling downsamples feature maps to reduce the spatial dimensions of the feature maps while retaining the essential information.

Pooling

Key objectives of pooling in CNNs:

1. Dimensionality Reduction:

2. Translation Invariance:

3. Robustness to Variations:

4. Extraction of Salient Features:

5. Spatial Hierarchy:

Common types of pooling

• Max pooling
  • selects the maximum value within each pooling region,
• Average pooling
  • calculates the average value.

Putting CNNs to work

source: MIT Course, http://introtodeeplearning.com/, L3

Summary: CNNs for classification

source: MIT Course, http://introtodeeplearning.com/, L3

Summary: CNNs for classification

source: MIT Course, http://introtodeeplearning.com/, L3

A toy example

The MNIST dataset

• A popular dataset or handwritten numbers.

library(keras)
mnist <- dataset_mnist()

• Made of features (images) and target values (labels)
• Divided into a training and test set.

x_train <- mnist$train$x; y_train <- mnist$train$y
x_test <- mnist$test$x; y_test <- mnist$test$y

(mnistDims <- dim(x_train))

[1] 60000    28    28

img_rows <- mnistDims[2];  img_cols <- mnistDims[3]

Data pre-processing (1): Reshaping

• These images are not in the the requires shape, as the number of channels is missing.
• This can be corrected using the array_reshape() function.

x_train <- array_reshape(x_train, c(nrow(x_train), img_rows, img_cols, 1))
x_test <- array_reshape(x_test, c(nrow(x_test), img_rows, img_cols, 1)) 

input_shape <- c(img_rows, img_cols, 1)

dim(x_train)

[1] 60000    28    28     1

Data pre-processing (2): Other transforms

• Data is first normalized (to values in [0,1])

x_train <- x_train / 255
x_test <- x_test / 255

• Labels are one-hot-encoded using the to_categorical() function.

num_classes = 10
y_train <- to_categorical(y_train, num_classes)
y_test <- to_categorical(y_test, num_classes)

Modeling (1): Definition

model <- keras_model_sequential() %>%
  layer_conv_2d(filters = 16,
                kernel_size = c(3,3),
                activation = 'relu',
                input_shape = input_shape) %>% 
  layer_max_pooling_2d(pool_size = c(2, 2)) %>% 
  layer_dropout(rate = 0.25) %>% 
  layer_flatten() %>% 
  layer_dense(units = 10,
              activation = 'relu') %>% 
  layer_dropout(rate = 0.5) %>% 
  layer_dense(units = num_classes,
              activation = 'softmax')

Modeling (1): Model Summary

model %>% summary()

Model: "sequential"
________________________________________________________________________________
 Layer (type)                       Output Shape                    Param #     
================================================================================
 conv2d (Conv2D)                    (None, 26, 26, 16)              160         
 max_pooling2d (MaxPooling2D)       (None, 13, 13, 16)              0           
 dropout_1 (Dropout)                (None, 13, 13, 16)              0           
 flatten (Flatten)                  (None, 2704)                    0           
 dense_1 (Dense)                    (None, 10)                      27050       
 dropout (Dropout)                  (None, 10)                      0           
 dense (Dense)                      (None, 10)                      110         
================================================================================
Total params: 27,320
Trainable params: 27,320
Non-trainable params: 0
________________________________________________________________________________

Modeling (2): Compilation

• Categorical cross-entropy as loss function.
• Adadelta optimizes the gradient descent.
• Accuracy serves as metric.

model %>% compile(
  loss = loss_categorical_crossentropy,
  optimizer = optimizer_adadelta(),
  metrics = c('accuracy')
)

Model training

• A mini-batch¹ size of 128 should allow the tensors to fit into the memory of most “normal” machines.
• The model will run over 12 epochs,
• With a validation split set at 0.2

batch_size <- 128
epochs <- 12

model %>% fit(
  x_train, y_train,
  batch_size = batch_size,
  epochs = epochs,
  validation_split = 0.2
)

1. • A batch is a collection of training examples processed together,
   • A minibatch is a smaller subset of a batch used for memory efficiency
   • An epoch is a complete pass of the entire training dataset during model training.

Model evaluation

• Use test data to evaluate the model.

model %>% evaluate(x_test, y_test)

    loss accuracy 
2.213136 0.225200 

predictions <- model %>% predict(x_test) # Not shown

References and Resources

Resources

Courses

• An introduction to Deep Learning. Alex Amini. MIT

Workshops

• Deep learning with R Summer course
• Deep learning with keras and Tensorflow in R (Rstudio conf. 2020)

Books

• Deep learning with R, 2nd edition. F. Chollet

Documents

• Introduction to Convolutional Neural Networks (CNN)
• Convolutional Neural Networks in R